Chaikin's corner cutting algorithm smooths a curve by iteratively replacing every point by two new points: one 1/4 of the way to the next point and one 1/4 of the way to the previous point.
smooth_chaikin(x, wrap = FALSE, refinements = 3L)Arguments
- x
numeric matrix; 2-column matrix of coordinates.
- wrap
logical; whether the coordinates should be wrapped at the ends, as for polygons and closed lines, to ensure a smooth edge.
- refinements
integer; number of corner cutting iterations to apply.
Value
A matrix with the coordinates of the smoothed curve.
Details
This function works on matrices of points and is generally not called
directly. Instead, use smooth() with method = "chaikin" to apply this
smoothing algorithm to spatial features.
References
The original reference for Chaikin's corner cutting algorithm is:
Chaikin, G. An algorithm for high speed curve generation. Computer Graphics and Image Processing 3 (1974), 346–349
This implementation was inspired by the following StackOverflow answer:
See also
Examples
# smooth_chaikin works on matrices of coordinates
# use the matrix of coordinates defining a polygon as an example
m <- jagged_polygons$geometry[[2]][[1]]
m_smooth <- smooth_chaikin(m, wrap = TRUE)
class(m)
#> [1] "matrix" "array"
class(m_smooth)
#> [1] "matrix" "array"
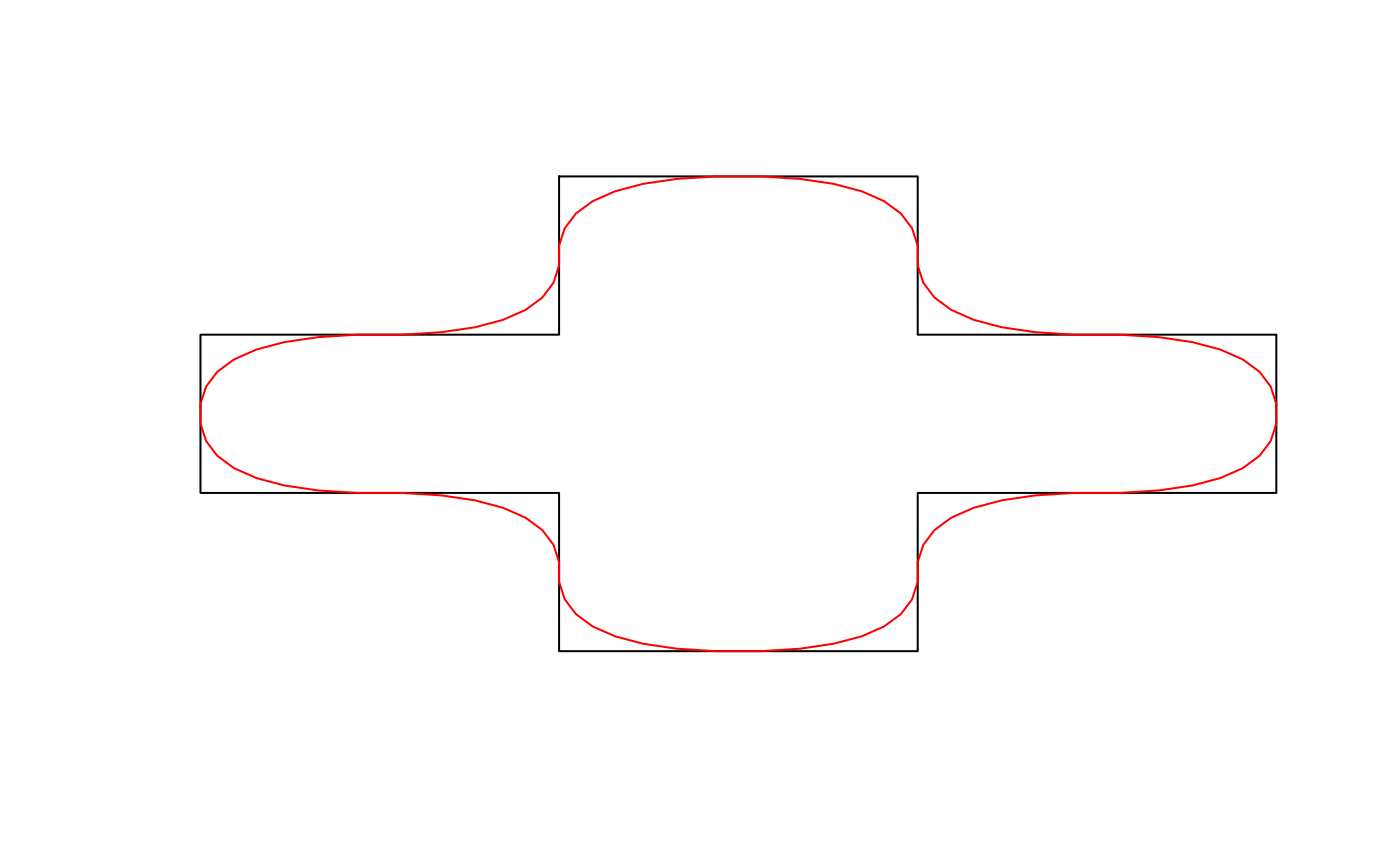
plot(m, type = "l", axes = FALSE, xlab = NA, ylab = NA)
lines(m_smooth, col = "red")
# smooth is a wrapper for smooth_chaikin that works on spatial features
library(sf)
p <- jagged_polygons$geometry[[2]]
p_smooth <- smooth(p, method = "chaikin")
class(p)
#> [1] "XY" "POLYGON" "sfg"
class(p_smooth)
#> [1] "XY" "POLYGON" "sfg"
plot(p)
plot(p_smooth, border = "red", add = TRUE)
