Densify lines or polygons

This function adds additional vertices to lines or polygons via linear interpolation, always while keeping the original vertices. Each line segment will be split into equal length sub-segments. This densification algorithm treats all vertices as Euclidean points, i.e. new points will not fall on a great circle between existing vertices, rather they'll be along a straight line.

smooth_densify(x, wrap = FALSE, n = 10L, max_distance)

Arguments

x

numeric matrix; matrix of coordinates.

wrap

logical; whether the coordinates should be wrapped at the ends, as for polygons and closed lines, to ensure a smooth edge.

n

integer; number of times to split each line segment. Ignored if max_distance is specified.

max_distance

numeric; the maximum distance between vertices in the resulting matrix. This is the Euclidean distance and not the great circle distance.

Value

A matrix with the coordinates of the densified curve.

Details

This function works on matrices of points and is generally not called directly. Instead, use smooth() with method = "densify" to apply this smoothing algorithm to spatial features.

Examples

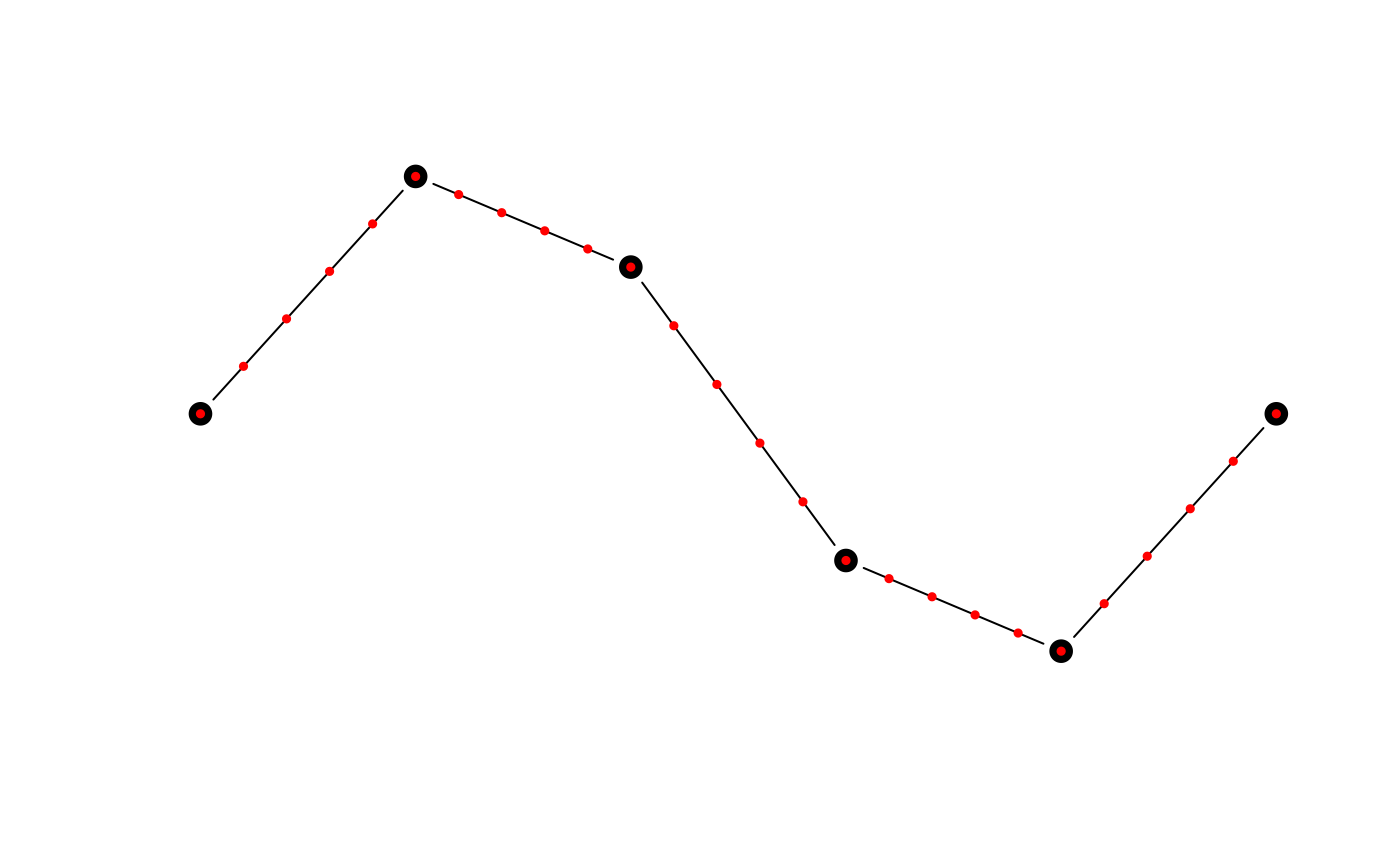
# smooth_densify works on matrices of coordinates
# use the matrix of coordinates defining a line as an example
m <- jagged_lines$geometry[[2]][]
m_dense <- smooth_densify(m, n = 5)
class(m)
#> [1] "matrix" "array" 
class(m_dense)
#> [1] "matrix" "array" 
plot(m, type = "b", pch = 19, cex = 1.5, axes = FALSE, xlab = NA, ylab = NA)
points(m_dense, col = "red", pch = 19, cex = 0.5)


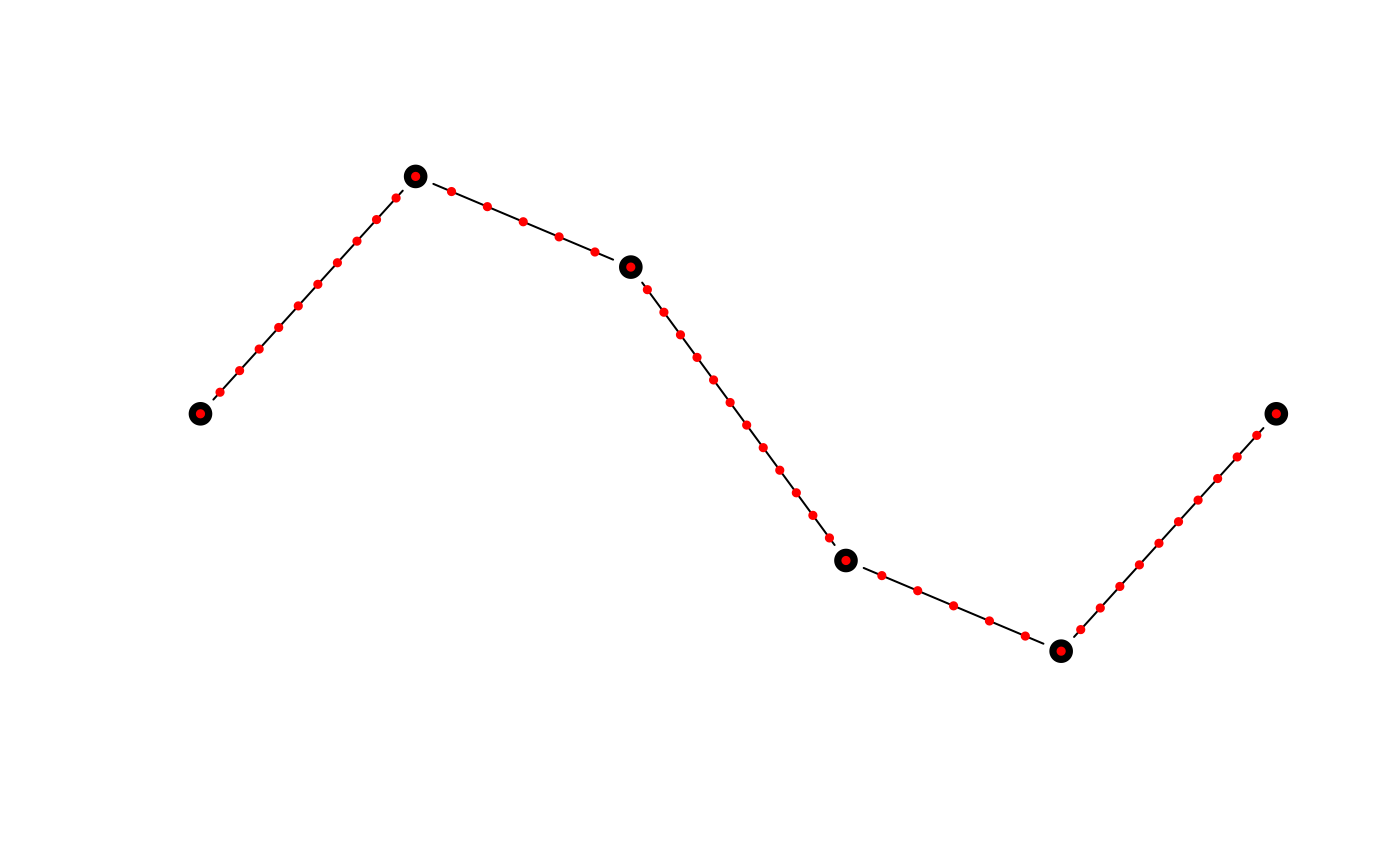
# max_distance can be used to ensure vertices are at most a given dist apart
m_md <- smooth_densify(m, max_distance = 0.05)
plot(m, type = "b", pch = 19, cex = 1.5, axes = FALSE, xlab = NA, ylab = NA)
points(m_md, col = "red", pch = 19, cex = 0.5)


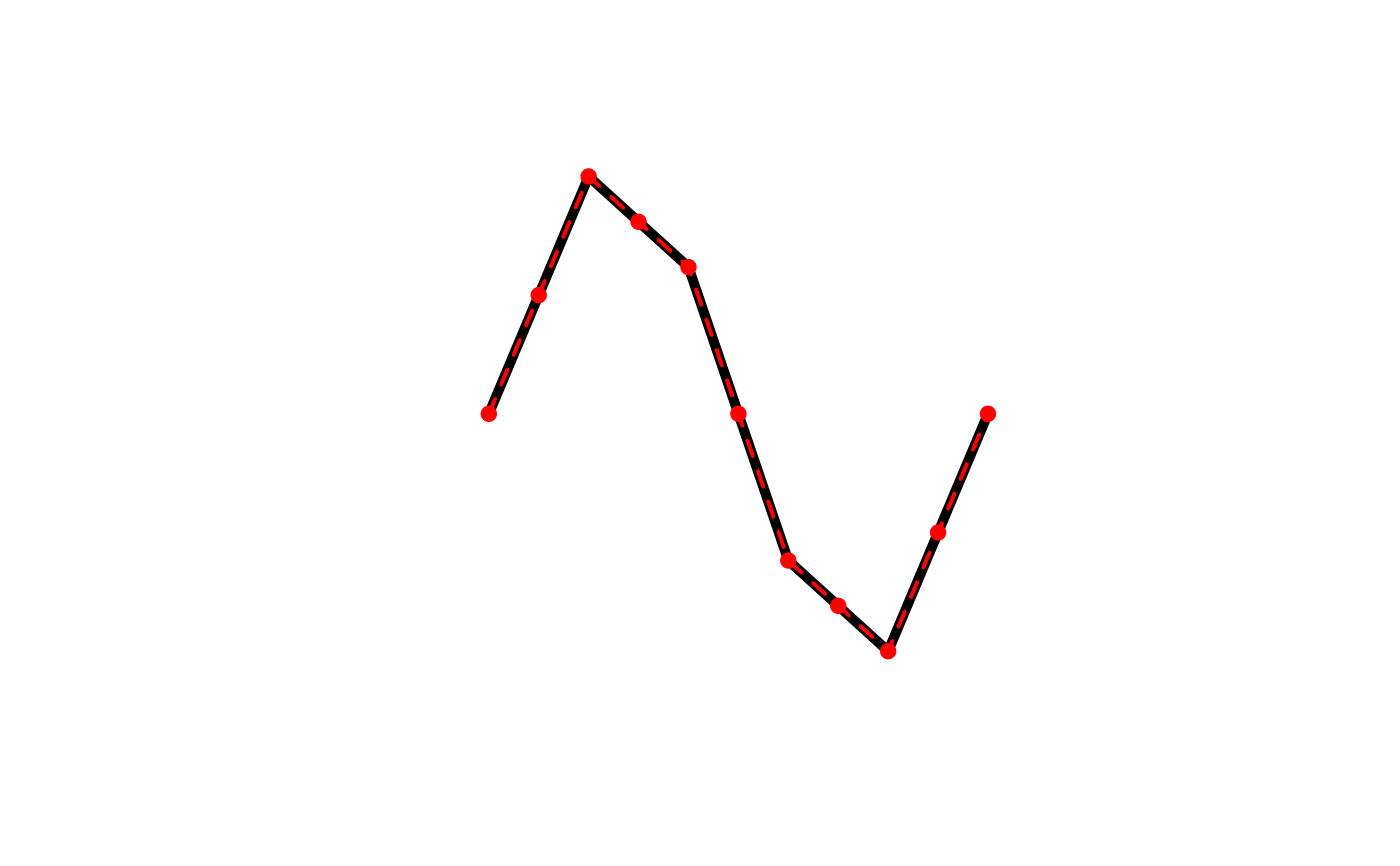
# smooth is a wrapper for smooth_densify that works on spatial features
library(sf)
l <- jagged_lines$geometry[[2]]
l_dense <- smooth(l, method = "densify", n = 2)
class(l)
#> [1] "XY"         "LINESTRING" "sfg"       
class(l_dense)
#> [1] "XY"         "LINESTRING" "sfg"       
plot(l, lwd = 5)
plot(l_dense, col = "red", lwd = 2, lty = 2, add = TRUE)
plot(l_dense %>% st_cast("MULTIPOINT"), col = "red", pch = 19,
     add = TRUE)